“经济控制论“一词是在1952年巴黎召开的世界控制论大会上首先提出的。
1954年,美国数学家R.S.菲利普斯开始用二阶常微分方程描述宏观经济系统,并讨论了系统的开环控制和闭环控制问题,采用PID(比例-积分-微分)控制原理来改善经济政策的稳定性。
50年代中期,美国H.A.西蒙等人研究了宏观经济的最优控制问题。
50年代末,波兰科学院应用控制理论的方法建立中央国民经济计划系统模型。
几十年来,在许多控制理论家、经济学家、数学家等的共同合作和努力探索下已取得显著成果,并于1975年在布加勒斯特召开的第三届国际控制论与系统大会上正式确认经济控制论这一新兴学科。
PID(比例(proportion)、积分(integration)、微分(differentiation))控制器作为最早实用化的控制器已有近百年历史,现在仍然是应用最广泛的工业控制器。PID控制器简单易懂,使用中不需精确的系统模型等先决条件,因而成为应用最为广泛的控制器。
PID控制器由比例单元(P)、积分单元(I)和微分单元(D)组成。其输入e (t)与输出u(t)的关系为u(t)=kp[e(t)+1/TI∫e(t)dt+TD*de(t)/dt] 式中积分的上下限分别是0和t 因此它的传递函数为:G(s)=U(s)/E(s)=kp[1+1/(TI*s)+TD*s] 其中kp为比例系数;TI为积分时间常数;TD为微分时间常数。

用更专业的话来讲,一个PID控制器可以被称作一个在频域系统的滤波器,这一点在计算它是否会最终达到稳定结果时很有用。如果数值挑选不当,控制系统的输入值会反复振荡,这导致系统可能永远无法达到预设值。
比例控制是一种最简单的控制方式,其控制器的输出与输入误差信号成比例关系。
作用:一种最简单的调节规律,调节器的输出u(t)与输入偏差e(t)成正比,只要出现偏差e(t),就能及时地产生与之成比例的调节作用。其作用大小,除与偏差e(t)有关外,主要取决与比例系数Kp,Kp越大,调节作用越强,动态特性也越好,反之,Kp越小,调节作用越弱。
但对于大多数惯性环节,Kp太大,会引起自激振荡。
缺点:存在静差,是有差调节,对于扰动较大,且惯性也较大的系统,若采用单纯的比例调节,则很难兼顾动态和静态特性。
我们可以把股市点位抽象成一个二阶系统, 合作杠杆的加入实际上就是人为的加入了一个比例环节。leverage杠杆的倍数实际上就是比例环节P的倍数,那么对一个典型的二阶系统, 加大比例环节的后对冲击响应(可以理解为利好性消息)的反应为:
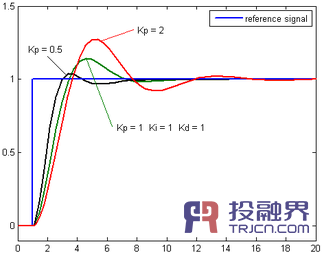
也就是说,加入合作杠杆后,股市的波动幅度会非常的剧烈,如果杠杆比例一味增加,可能导致系统震荡。
同样的,pid理论也可以预测T+0之后的股市的走向, 相当于缩短系统的时间常数Ts。





